Controle Estatístico de Processos: Ferramentas Estatísticas para Análise de Relatórios de Prevenção de Acidentes na Aviação do Exército

Introdução

Não se pode administrar o que não se pode medir." - Morris A. Cohen

O presente artigo tem por objetivo apresentar uma breve análise sobre o uso de ferramentas de Controle Estatístico de Processos (CEP) na interpretação de séries históricas de Relatórios de Prevenção de Acidentes Aeronáuticos (RELPREV). Ao final, as ferramentas em discussão serão exemplificadas com o uso de dados reais fornecidos pela Seção de Investigação e Prevenção de Acidentes Aeronáuticos, do Comando de Aviação do Exército (SIPAA/CAvEx).

Este artigo apresentará uma proposta para a identificação de fenômenos por meio do monitoramento de dados organizados sob a forma de Gráficos de Controle para Variáveis, tipo “Gráficos de Shewhart”, como ferramenta auxiliar para a tomada de medidas mitigadoras, de modo que uma série histórica de RELPREV mantenha-se sob controle estatístico.

Desenvolvimento

Os gráficos de controle foram desenvolvidos na década de 1920 pelo Dr. Walter A. Shewhart, do Bell Telephone Laboratories e seus conceitos estatísticos são considerados por Montgomery como a base do CEP.

Considera-se que um sistema está sob controle estatístico se as variações do processo, aleatórias, ocorrem de forma naturalmente estável. As variabilidades que não possuem causas aleatórias são consideradas sob ação de causas atribuíveis e apresentarão um padrão que permite caracterizar o processo como fora de controle.

Os dados distribuídos num gráfico de controle serão analisados conforme sua dispersão em torno de uma linha central (uma média), dentro de um intervalo de confiança medido em valores múltiplos do desvio padrão apresentado pela amostra. A média (µ) e o desvio padrão (σ) são também conhecidos como estatísticas do processo. Tais estatísticas são deslocadas dos seus valores nominais (denominados alvos) se o processo tender a sair do controle.

O intervalo de confiança será limitado acima e abaixo da linha central por limites de controle (LC). Esses limites são conhecidos por “três-sigma”, pois tipicamente estão a 3 vezes o valor do desvio-padrão acima e abaixo do valor médio.

Considerando-se “L” como uma “distância” entre os limites de controle (superior - LSC; inferior - LIC) e a linha central, teremos:

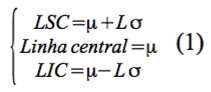
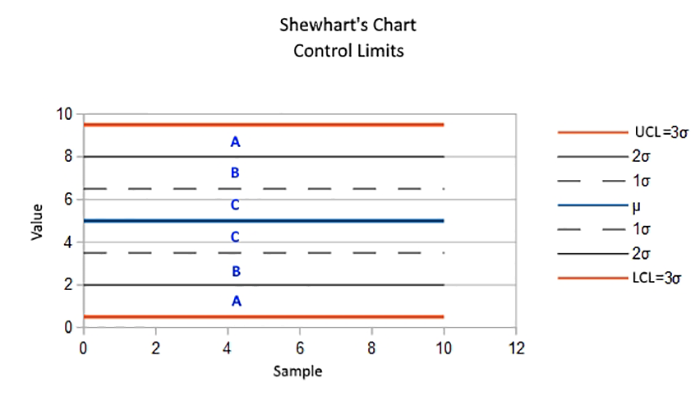
Chamaremos de “zona C” aquela compreendida entre os limites de controle 1σ. A “zona B” será delimitada pelos limites 2σ, excluindo-se a zona C. A “zona A” será delimitada pelos limites 3σ, excluindo-se as zonas B e C. Os limites 2σ serão definidos como “limites de alerta”. A Fig.1 ilustrará tais zonas.

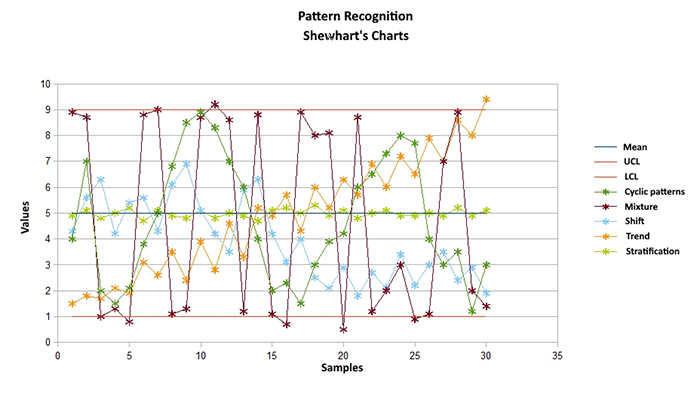
A distribuição de pontos no gráfico permite a identificação de um padrão. O reconhecimento desse padrão é o problema-chave na identificação de razões para o comportamento não-aleatório do processo (fora de controle). Montgomery apresenta as seguintes regras sensibilizantes para a identificação dos padrões:

1. Um ponto se localiza fora dos limites de controle;
2. Dois, em três pontos consecutivos, se localizam além dos limites de alerta (2σ);
3. Quatro, em cinco pontos consecutivos, se localizam a uma distância de 1σ ou mais em relação à linha central;
4. Oito pontos consecutivos se localizam de um mesmo lado da linha central;
5. Seis pontos em uma sequência sempre crescente ou decrescente;
6. Quinze pontos em sequência na zona C;
7. Quatorze pontos em sequência alternadamente para cima e para baixo;
8. Oito pontos em sequência de ambos os lados da linha central, com nenhum na zona C;
9. Um padrão não-usual ou não-aleatório nos dados; ou
10. Um ou mais pontos perto de um limite de alerta ou de controle.

Ressalta-se que quanto mais pontos plotados, maior a capacidade de análise.

A interpretação desses padrões, para fins práticos, se inicia com a análise de um gráfico de observações individuais, seguida pela análise de um gráfico de amplitudes. Para amostras caracterizadas pelo tamanho n_A = 1 – como é o caso das amostragens anuais de quantidade de RELPREV – empregaremos a técnica de amplitude móvel (MR), onde MR é definida pela equação 2 e “i” é a ordem de amostragem, com i ∈ ΙN^∗ ∧ i ≠ 1.

MR_i = Ιx_i - x_{i - 1}Ι (2)

A construção do gráfico das amplitudes considerará os parâmetros D₃ = 0 e D₄ = 3,267, para amplitude n_MR = 2. Esses valores são tabelados, calculáveis, e estão disponíveis no Apêndice VI da literatura de referência. A equação 3 apresentará os parâmetros de controle, onde a “barra” indica um valor médio da série.

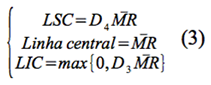
A construção do gráfico de controle para as observações individuais (RELPREV) segue a equação 1, onde:

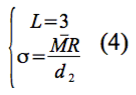
Sendo d₂ = 1,128 a média da amplitude relativa, tabelada na literatura de referência.

As linhas denominadas “alerta” serão quantificadas pelos valores de L = 2, i.e., ±2σ.

Antes de serem analisados os padrões no gráfico de RELPREV, o analista deverá se certificar que o gráfico de MR está sob controle. Se ambos os gráficos estiverem fora de controle, o analista deverá propor medidas que eliminem primeiro as causas atribuíveis ao gráfico MR, o que geralmente corrige o gráfico associado ao RELPREV.

Poderão ser observados os seguintes padrões:

• Padrões cíclicos – pode ser resultado de mudanças sistemáticas (fadiga humana, consequência de ações gerenciais, “curva de sangue”, etc.);
• Mistura – pode ser resultado de “supercontrole” (ajustes muito frequentes nos procedimentos, respondendo a variações aleatórias na saída e não nas causas atribuíveis);
• Deslocamento do nível do processo – pode ser resultado da introdução de novos métodos de inspeção e de execução, mudança de cultura organizacional, mudança de referências na segurança de voo, mudança nas habilidades, na atenção ou na motivação do pessoal gerador de RELPREV;
• Tendência – pode ser resultado de uma deterioração gradual de um componente crítico do processo, da fadiga humana, do aumento ou da diminuição da ação supervisória, de fatores sazonais (dentro de um ano: períodos de férias, grandes substituições de equipes, condições meteorológicas rigorosas);
• Estratificação – propensão dos pontos se agruparem artificialmente muito próximos à linha central. Pode ser resultado do cálculo incorreto dos limites de controle ou de amostragem com unidades diferentes. Por exemplo: se a amostra considerar uma quantidade de RELPREV cujas ocorrências possuam frequências demasiadamente díspares (fator operacional versus fator material), a variabilidade da mais frequente “mascara” a variabilidade da menos frequente, quantificando incorretamente a variabilidade entre ambas.

A Figura 2 ilustrará tais padrões.

Análise de Dados Reais

Os dados da Tabela 1 foram fornecidos pela SIPAA/CAvEx e apresentam os quantitativos de RELPREV emitidos nos respectivos anos.

Foram consideradas as seguintes hipóteses: a distribuição é normal, os valores obtidos são independentes no período (não correlacionados), os alvos do processo foram obtidos pelo tratamento da amostra dos 26 últimos anos e os limites são igualmente espaçados da linha central (exceção: LIC < 0 ⇒ LIC = 0). A amostragem é regular (anual, cíclica) e os dados são valores inteiros discretos (não há que se considerar “0,75 RELPREV”, por exemplo).

Os gráficos a seguir foram obtidos pelo tratamento de dados no programa Apache OpenOffice™ Calc 4.1.1, utilizando-se a metodologia citada neste artigo.

Conclusão

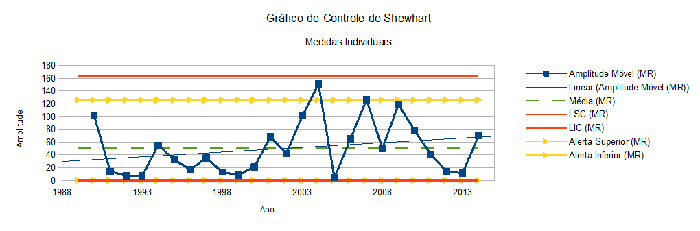
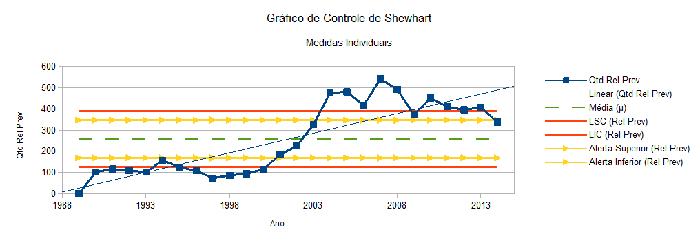
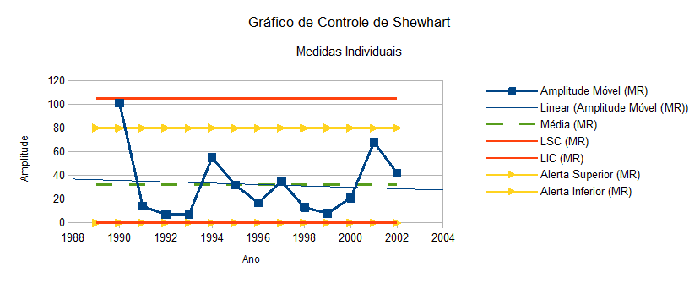
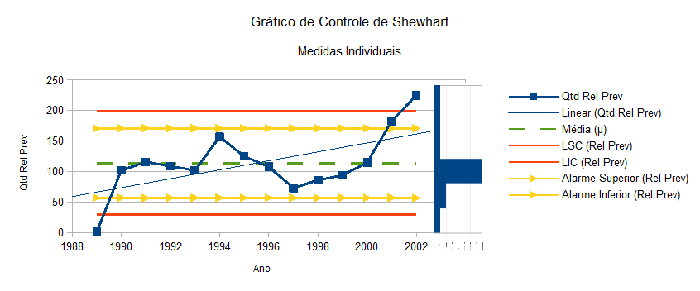
A análise da Figura 4 permite concluir que o gráfico da série histórica deslocou o nível do processo em 2004, atingindo um novo patamar de valores médios a partir de então.

Para melhor compreensão dos dados considerando-se o referido deslocamento, a série histórica foi dividida em 2 períodos com estatísticas distintas: 1998 - 2002 e 2003 - 2014.

Um analista em 2003, utilizando essa técnica, teria condições de detectar no gráfico de RELPREV (Figura 6) os seguintes indícios de padrões fora de controle estatístico:

• um alerta em 2001;
• uma ultrapassagem de LSC ocorrida em 2002;
• um padrão cíclico a partir de 1993;
• um enquadramento na regra sensibilizante 5, referente aos pontos de 1997 a 2002.

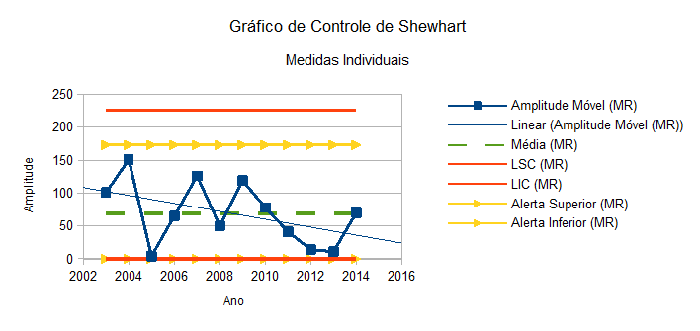
O gráfico de MR atual (Figura 7) apresentou 2 pontos (2012 e 2013) próximos ao limite inferior de alerta, requerendo atenção especial segundo a regra sensibilizante 10. Todavia, MR apresentou um favorável retorno à média em 2014.

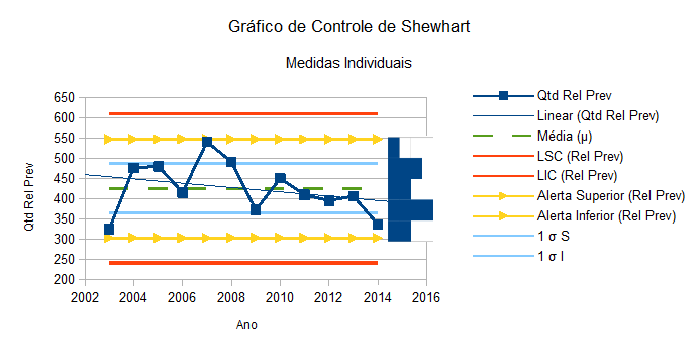
A série histórica atual apresenta um ponto próximo ao “alerta” (regra sensibilizante 10) no ano de 2014. Há uma tendência de decréscimo de RELPREV no período amostrado e um possível novo deslocamento do nível do processo, indicado pelo histograma lateral.

O uso dos gráficos de controle de Shewhart pode ser uma importante ferramenta preditiva de tendências na avaliação quantitativa de RELPREV. Recomenda-se que seu uso seja combinado com outras ferramentas, apresentadas por Montgomery, nas páginas 95 e 109. ♦

SOBRE O AUTOR